Introduction to Thermodynamics:

1. Thermodynamic System and Its Types

• Isolated System: No exchange of energy or matter with its surroundings. Example: The universe as a whole.
• Closed System: Energy can be exchanged with the surroundings, but matter cannot. Example: A sealed steam boiler.
• Open System: Both energy and matter can be exchanged with the surroundings. Example: A boiling pot of water.

2. Macroscopic vs. Microscopic Viewpoint

2.1 Macroscopic Viewpoint

2.2 Microscopic Viewpoint

3. Properties, Processes, and Cycles

3.1 Properties

• Intensive Properties: Independent of the amount of matter. Examples: Temperature, pressure, density.
• Extensive Properties: Dependent on the amount of matter. Examples: Volume, internal energy, mass.

3.2 Processes

• Isothermal Process: Occurs at constant temperature. Example: Isothermal expansion of an ideal gas.
• Adiabatic Process: No heat exchange with the surroundings. Example: Adiabatic compression of a gas.
• Isobaric Process: Occurs at constant pressure. Example: Heating of a liquid at constant pressure.
• Isochoric Process: Occurs at constant volume. Example: Heating of a gas in a rigid container.

3.3 Cycles

• Carnot Cycle: A theoretical cycle consisting of two isothermal and two adiabatic processes, representing the most efficient cycle.
• Rankine Cycle: Used in steam power plants, consisting of isentropic compression, isobaric heat addition, isentropic expansion, and isobaric heat rejection.

4. Point Function vs. Path Function

4.1 Point Function

• Temperature (T): Describes the thermal state of the system.
• Pressure (P): Describes the force exerted per unit area.
• Internal Energy (U): The total energy contained within the system.

4.2 Path Function

• Work (W): Energy transferred due to a force acting over a distance.
• Heat (Q): Energy transferred due to a temperature difference.

5. Thermodynamic Equilibrium

• Thermal Equilibrium: No temperature difference exists within the system or with its surroundings.
• Mechanical Equilibrium: No net force acting within the system or on the boundary.
• Chemical Equilibrium: No net chemical reactions occur within the system.

6. Quasi-static Process

7. Work and Heat Transfer

7.1 Work Transferred

• Boundary Work: Work done when the boundary of the system moves. For example, in an expanding gas.
• Electrical Work: Work done by or on electrical systems.
• Mechanical Work: Work done by mechanical devices.

7.2 Heat Transfer

• Conduction: Transfer of heat through a solid material. Example: Heat flowing through a metal rod.
• Convection: Transfer of heat through fluid motion. Example: Warm air rising in a room.
• Radiation: Transfer of heat through electromagnetic waves. Example: Heat from the sun.

7.3 Temperature and Its Measurement

• Thermocouples: Measure temperature based on the voltage generated at the junction of two different metals.
• Resistance Temperature Detectors (RTDs): Measure temperature by changes in electrical resistance of a metal.
• Thermometers: Use expansion of liquids or gases. Example: Mercury thermometers.

8. Zeroth Law of Thermodynamics

9. Specific Heat and Latent Heat

9.1 Specific Heat

9.2 Latent Heat

9.3 Relationship between (C_P) and (C_V)

First Law of Thermodynamics

1. Overview

The First Law of Thermodynamics is a fundamental principle that establishes the relationship between heat, work, and energy. It is also known as the Law of Energy Conservation. This law states that energy cannot be created or destroyed; it can only be transformed from one form to another. In mathematical terms, it is expressed as:

where ΔU is the change in internal energy, Q is the heat added to the system, and W is the work done by the system.

2. First Law of Thermodynamics for a Closed System

2.1 Closed System

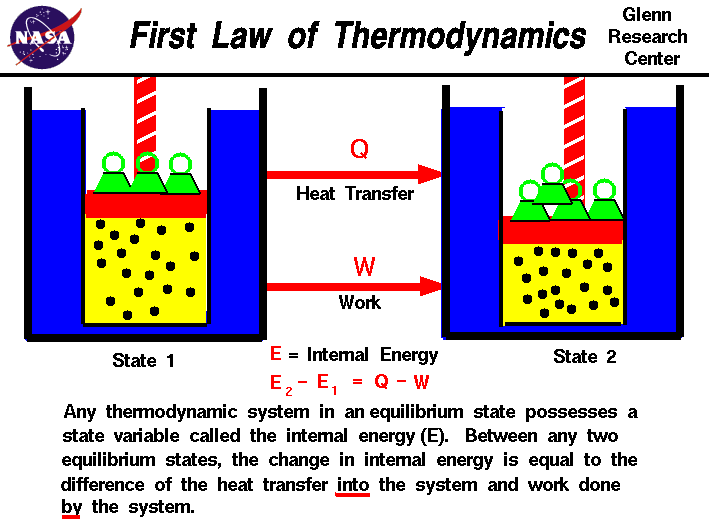
A closed system is one where matter cannot enter or leave, but energy in the form of heat or work can be transferred. For a closed system undergoing a change of state, the First Law of Thermodynamics can be applied as follows:

• Change of State: When a closed system undergoes a change in state, the energy transferred into the system as heat minus the work done by the system will result in a change in the internal energy of the system.
• Cycle: For a closed system undergoing a cyclic process, the net change in internal energy over one complete cycle is zero. Thus, the heat added to the system equals the work done by the system.

3. Energy and Its Forms

Energy in thermodynamics can be classified into several forms, including:

• • Kinetic Energy: The energy associated with the motion of the system.
  • Potential Energy: The energy associated with the position or configuration of the system.
  • Internal Energy: The total energy contained within the system, including the microscopic forms of energy such as molecular vibration and rotation.
  • Enthalpy (H): A thermodynamic property defined as the sum of internal energy and the product of pressure and volume:

where H is enthalpy, U is internal energy, P is pressure, and V is volume.

4. PMM-I and Control Volume

4.1 PMM-I (Perpetual Motion Machine of the First Kind)

PMM-I refers to a hypothetical machine that would create energy from nothing, violating the First Law of Thermodynamics. Such a machine is impossible as it contradicts the principle of energy conservation.

4.2 Control Volume

A control volume is a defined region in space through which energy and matter can flow. The First Law of Thermodynamics applied to a control volume involves:

• Mass Flow: Mass entering and leaving the control volume affects the energy balance.
• Energy Flow: Energy can be transferred into and out of the control volume in the form of heat and work.

5. Applications of the First Law in Steady Flow Processes

Steady flow processes involve fluids flowing through components such as nozzles, turbines, compressors, pumps, boilers, and throttle valves. The First Law of Thermodynamics is applied as follows:

• • Nozzle: A nozzle accelerates a fluid, converting enthalpy into kinetic energy. The First Law equation for a nozzle is:

where h1 and h2 are the specific enthalpies, and v1 and v2 are the velocities at the inlet and outlet, respectively.

• • Turbine: A turbine extracts work from a fluid flow. The First Law for a turbine can be written as:

where W_t is the work done by the turbine, and h1 and h2 are the specific enthalpies at the inlet and outlet, respectively.

• • Compressor: A compressor increases the pressure of a fluid by performing work on it. The First Law for a compressor is:

where W_c is the work done on the fluid, and h1 and h2 are the specific enthalpies at the inlet and outlet, respectively.

• • Pump: A pump increases the pressure of a liquid. The First Law for a pump is:

where W_p is the work done by the pump, and h1 and h2 are the specific enthalpies at the inlet and outlet, respectively.

• • Boiler: A boiler adds heat to a fluid, converting it into steam. The First Law for a boiler is:

where Q_b is the heat added, and h1 and h2 are the specific enthalpies before and after heating.

• • Throttle Valve: A throttle valve causes a pressure drop without adding or removing heat. The First Law for a throttle valve is:

where h1 and h2 are the specific enthalpies before and after throttling, respectively.

Second Law of Thermodynamics

1. Limitation of the First Law of Thermodynamics

The First Law of Thermodynamics, which states that energy cannot be created or destroyed, only transformed, does not provide information about the direction of energy transfer or the efficiency of energy conversion. It only accounts for the conservation of energy. The Second Law addresses these limitations by introducing the concept of entropy and the directionality of energy transfer.

2. Heat Engines, Refrigerators, and Heat Pumps

2.1 Heat Engine

A heat engine is a device that converts heat energy into mechanical work. It operates in a cyclic process and absorbs heat from a high-temperature source, performs work, and then releases some heat to a low-temperature sink. The efficiency (\( \eta \)) of a heat engine is given by:

where \( Q_h \) is the heat absorbed from the hot reservoir, and \( Q_c \) is the heat rejected to the cold reservoir.

2.2 Refrigerator

A refrigerator is a device that transfers heat from a low-temperature region to a high-temperature region, using work input. The performance of a refrigerator is measured by its coefficient of performance (COP), given by:

where \( Q_c \) is the heat removed from the cold reservoir, and \( W \) is the work input.

2.3 Heat Pump

A heat pump transfers heat from a low-temperature source to a high-temperature sink, using work input. Its performance is measured by its coefficient of performance (COP), given by:

where \( Q_h \) is the heat delivered to the hot reservoir, and \( W \) is the work input.

3. Kelvin-Planck and Clausius Statements

3.1 Kelvin-Planck Statement

The Kelvin-Planck statement of the Second Law of Thermodynamics asserts that it is impossible to construct a heat engine that operates in a cyclic process and converts all the heat absorbed from the hot reservoir into work, with no other effect (i.e., no heat rejected to the cold reservoir).

3.2 Clausius Statement

The Clausius statement asserts that it is impossible to construct a refrigerator or heat pump that, operating in a cyclic process, transfers heat from a cold reservoir to a hot reservoir without any work input.

3.3 Equivalence of Kelvin-Planck and Clausius Statements

Both statements are equivalent; proving one implies the validity of the other. This equivalence underscores the fundamental constraints imposed by the Second Law of Thermodynamics on energy conversion and transfer processes.

4. Reversibility and Irreversibility

4.1 Reversibility

A process is reversible if it can be reversed without leaving any net change in the system or its surroundings. In other words, both the system and surroundings must be restored to their original states without any entropy increase.

4.2 Irreversibility

Irreversible processes involve some form of energy dissipation, such as friction, unrestrained expansion, or heat transfer through a finite temperature difference. These processes result in an increase in entropy and cannot be reversed without external intervention.

5. Carnot Cycle and Carnot Theorem

5.1 Carnot Cycle

The Carnot cycle is an idealized thermodynamic cycle consisting of two isothermal processes and two adiabatic processes. It is the most efficient cycle possible for a heat engine operating between two thermal reservoirs. The Carnot cycle consists of:

• Isothermal Expansion: The gas absorbs heat \( Q_h \) from the hot reservoir at a constant temperature \( T_h \).
• Adiabatic Expansion: The gas expands adiabatically, doing work on the surroundings and cooling down to temperature \( T_c \).
• Isothermal Compression: The gas releases heat \( Q_c \) to the cold reservoir at a constant temperature \( T_c \).
• Adiabatic Compression: The gas is compressed adiabatically, increasing its temperature back to \( T_h \).

5.2 Carnot Theorem

The Carnot theorem states that no heat engine operating between two heat reservoirs can be more efficient than a Carnot engine operating between the same reservoirs. The efficiency of a Carnot engine is given by:

where \( T_h \) and \( T_c \) are the absolute temperatures of the hot and cold reservoirs, respectively.

6. Absolute Thermodynamic Temperature Scale

The absolute temperature scale, also known as the Kelvin scale, is based on the concept of absolute zero, the temperature at which a perfect gas would have zero volume and no kinetic energy. The absolute temperature \( T \) is measured in Kelvin (K) and is related to the Celsius temperature \( T_C \) by:

7. Entropy

7.1 Introduction

Entropy is a measure of the disorder or randomness in a system. It quantifies the amount of energy in a system that is not available for doing useful work. Entropy increases in natural processes, reflecting the tendency for systems to evolve towards greater disorder.

7.2 Clausius Theorem

The Clausius theorem states that for a reversible process, the change in entropy (\( ΔS \)) is equal to the heat transferred divided by the temperature:

where \( Q \) is the heat added and \( T \) is the temperature at which the heat is added.

7.3 T-S Plot

A temperature-entropy (T-S) plot is a graphical representation of the entropy changes in a thermodynamic process. The area under the curve in a T-S plot represents the heat added or removed during the process.

7.4 Clausius Inequality

The Clausius inequality states that for any real (irreversible) process, the change in entropy (\( ΔS \)) is greater than or equal to the heat transferred divided by the temperature:

7.5 Entropy and Irreversibility

Entropy is a measure of irreversibility in a process. An increase in entropy indicates the presence of irreversible effects such as friction, mixing, or heat transfer across a temperature gradient.

7.6 Entropy Principle and Its Application

The entropy principle asserts that in any natural process, the total entropy of a closed system always increases. This principle is used to analyze and predict the feasibility of thermodynamic processes and to understand the direction of spontaneous processes.

7.7 Combined I and II Law

The combined first and second laws of thermodynamics provide a comprehensive framework for understanding energy transformations. They state that energy is conserved (First Law) and that energy transformations are constrained by the increase in entropy (Second Law).

7.8 Entropy and Disorder

Entropy is often associated with disorder. In thermodynamic systems, an increase in entropy corresponds to an increase in disorder or randomness. The entropy of a system provides a quantitative measure of this disorder.

Ideal Gas Law

1. Introduction to Ideal Gases

An ideal gas is a hypothetical gas that perfectly follows the gas laws under all conditions. The ideal gas law is a fundamental equation that describes the behavior of such gases. It assumes that gas molecules do not interact with each other except through elastic collisions, and the volume of the gas molecules is negligible compared to the volume of the container.

2. Boyle’s Law

Boyle’s Law states that the pressure of a given mass of gas is inversely proportional to its volume when temperature is held constant. Mathematically, it is expressed as:

where \( P1 \) and \( P2 \) are the initial and final pressures, and \( V1 \) and \( V2 \) are the initial and final volumes, respectively. This law reflects the inverse relationship between pressure and volume for a constant amount of gas at constant temperature.

3. Charles’s Law

Charles’s Law states that the volume of a given mass of gas is directly proportional to its absolute temperature when pressure is held constant. It is mathematically expressed as:

where \( V1 \) and \( V2 \) are the initial and final volumes, and \( T1 \) and \( T2 \) are the initial and final absolute temperatures (measured in Kelvin). This law indicates that as temperature increases, the volume of the gas expands, provided the pressure remains constant.

4. Avogadro’s Law

Avogadro’s Law states that the volume of a gas at constant temperature and pressure is directly proportional to the number of moles of gas. Mathematically, it is expressed as:

where \( V \) is the volume, \( n \) is the number of moles, and \( k \) is a constant. This law implies that equal volumes of different gases, at the same temperature and pressure, contain the same number of molecules.

5. Universal Gas Constant

The universal gas constant \( R \) is a constant that appears in the ideal gas law equation. It relates the energy scale to the temperature scale in gas calculations. The ideal gas law is given by:

where \( P \) is the pressure, \( V \) is the volume, \( n \) is the number of moles of gas, \( R \) is the universal gas constant, and \( T \) is the absolute temperature. The value of \( R \) is approximately:

This constant ensures that the units are consistent in the ideal gas law equation.

6. Ideal Processes

Ideal processes refer to theoretical processes where gases follow the ideal gas law perfectly. Common ideal processes include:

• • Isothermal Process: A process in which the temperature of the gas remains constant. During an isothermal process, the internal energy of the gas does not change, and the work done by or on the gas is given by:

• • Adiabatic Process: A process in which no heat is exchanged with the surroundings. For an adiabatic process, the relationship between pressure and volume is given by:

where \( γ \) (gamma) is the adiabatic index, \( γ = C_p / C_v \), with \( C_p \) being the specific heat at constant pressure and \( C_v \) being the specific heat at constant volume.

• • Isochoric Process: A process where the volume remains constant. During this process, the pressure of the gas changes with temperature according to:

• • Isobaric Process: A process where the pressure remains constant. The volume of the gas changes linearly with temperature:

7. Other Equations of State

While the ideal gas law provides a good approximation for many gases under a range of conditions, real gases deviate from ideal behavior under high pressure and low temperature. Several other equations of state account for these deviations:

• • Van der Waals Equation: An equation that accounts for the finite size of molecules and the intermolecular forces. It is given by:

where \( a \) and \( b \) are constants specific to each gas, accounting for intermolecular attractions and molecular volume, respectively.

• • Redlich-Kwong Equation: A more complex equation that improves on the Van der Waals equation by including additional terms for better accuracy at higher pressures:

Properties of Pure Substance

1. Phase Change Phenomenon

The phase change phenomenon refers to the transition of a substance from one phase to another, such as from solid to liquid (melting), liquid to gas (vaporization), or vice versa. For a pure substance, these transitions occur at specific temperatures and pressures and are represented on a phase diagram.

2. Phase Diagram of Pure Substance

A phase diagram is a graphical representation of the physical states of a substance under different conditions of temperature and pressure. It consists of three main regions:

• Solid: Region where the substance is in the solid phase.
• Liquid: Region where the substance is in the liquid phase.
• Gas: Region where the substance is in the gaseous phase.

The phase diagram also includes lines called phase boundaries, which indicate the conditions under which two phases coexist. Key points on the diagram include:

• Triple Point: The unique set of conditions (temperature and pressure) at which all three phases (solid, liquid, and gas) coexist in equilibrium.
• Critical Point: The temperature and pressure at which the liquid and gas phases become indistinguishable, resulting in a supercritical fluid.

3. P-v, T-s, and h-s Diagrams

These diagrams are useful for analyzing the thermodynamic properties of pure substances and processes involving them:

• P-v Diagram: A pressure-volume diagram showing the relationship between pressure (P) and volume (v) of the substance. It includes isothermal and isobaric lines, as well as phase boundaries.
• T-s Diagram: A temperature-entropy diagram where temperature (T) is plotted against entropy (s). This diagram helps visualize processes like heating, cooling, and phase changes.
• h-s Diagram: An enthalpy-entropy diagram showing the relationship between enthalpy (h) and entropy (s). It is used to analyze energy changes and efficiencies in thermodynamic cycles.

4. Properties of Steam

Steam is the gaseous phase of water and has specific properties that are crucial for thermodynamic analysis:

• Saturation Temperature: The temperature at which steam is in equilibrium with liquid water at a given pressure.
• Saturation Pressure: The pressure at which steam is in equilibrium with liquid water at a given temperature.
• Specific Volume: The volume occupied by a unit mass of steam, typically measured in cubic meters per kilogram (m³/kg).
• Enthalpy: The total heat content of steam, including internal energy and work done. It is measured in kilojoules per kilogram (kJ/kg).

5. Critical Point Parameters

The critical point is characterized by the critical temperature and critical pressure. At this point, the properties of the liquid and gas phases become indistinguishable, and the substance becomes a supercritical fluid. The critical parameters are:

• Critical Temperature (T_c): The highest temperature at which the substance can exist as a liquid.
• Critical Pressure (P_c): The pressure required to maintain the substance in the liquid phase at the critical temperature.

6. Property Table

A property table provides detailed information about a substance’s thermodynamic properties at various temperatures and pressures. For steam, the property table includes values for:

• Saturation temperature and pressure
• Specific volume (v_f, v_g, and v_fg)
• Enthalpy (h_f, h_g, and h_fg)
• Entropy (s_f, s_g, and s_fg)

7. Representation of Processes on Diagrams

Processes involving steam can be represented on various diagrams to analyze the thermodynamic changes:

• P-v Diagram: Shows how pressure and volume change during processes like compression, expansion, and phase changes.
• T-s Diagram: Illustrates changes in temperature and entropy during processes such as heating, cooling, and phase transitions.
• h-s Diagram: Used to represent energy changes in processes like isentropic expansion, isobaric heating, and isothermal compression.

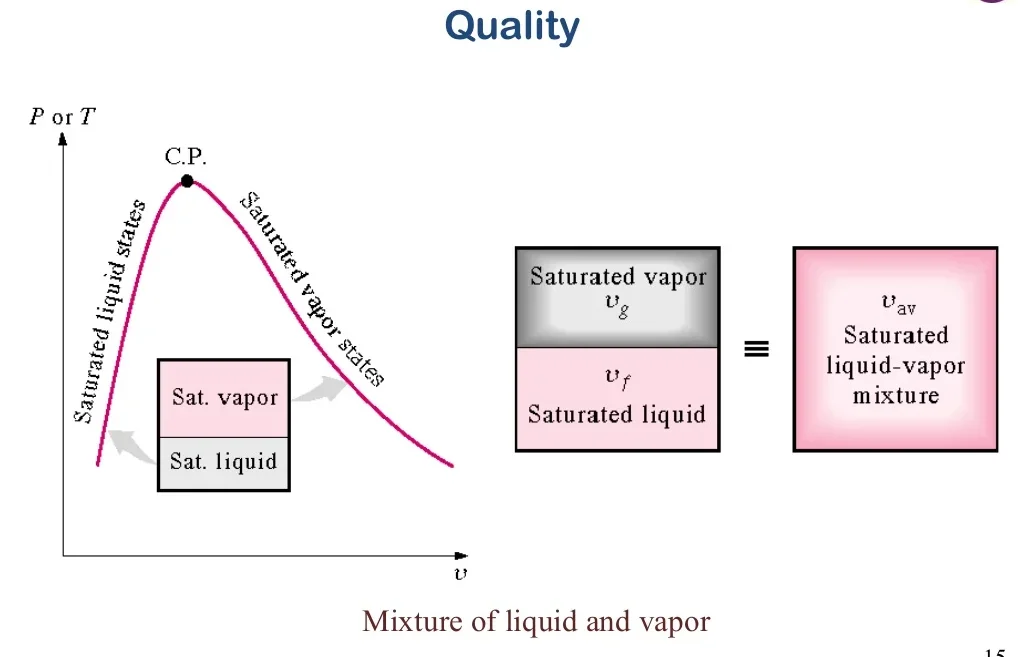
8. Dryness Fraction and Its Measurement

The dryness fraction (x) is a measure of the amount of vapor present in a steam-water mixture. It is defined as the ratio of the mass of vapor to the total mass of the mixture:

where \( m_v \) is the mass of the vapor and \( m_l \) is the mass of the liquid. The dryness fraction can be measured using:

• Throttling Calorimeter: A device that measures the change in enthalpy to determine the dryness fraction.
• Separating Calorimeter: A device that separates the vapor and liquid phases to measure their masses and calculate the dryness fraction.