Unit 1: Complex Numbers

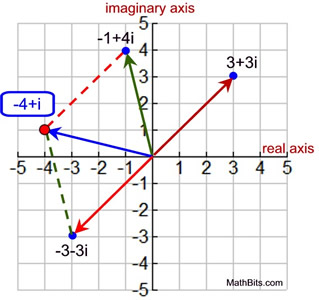
1. Definition and Geometrical Representation

A complex number is an extension of the real number system, where real numbers are supplemented by an imaginary component. A general complex number is of the form:

Where:

• z = Complex number
• x = Real part
• y = Imaginary part
• i = Imaginary unit, where \( i^2 = -1 \)

This means that the square of the imaginary unit \(i\) is negative one, introducing the concept of numbers outside the real number line.

The complex number can be represented geometrically on a 2D plane (called the Argand plane) where the real part lies on the x-axis, and the imaginary part lies on the y-axis. The modulus (or magnitude) of the complex number is given by:

This formula represents the distance from the origin to the point (x, y) in the complex plane. Complex numbers are useful in representing quantities that have both magnitude and direction, such as forces in physics or waves in electrical engineering.

2. Polar Form of Complex Numbers

A complex number can also be represented in polar form, where instead of using rectangular coordinates (x, y), we use the modulus \(r\) and the argument (angle) \(θ\). The polar form of a complex number is written as:

Where:

• r = Magnitude or modulus of the complex number, \(r = √(x² + y²)\)
• θ = Argument of the complex number, \(θ = \tan^{-1}(y/x)\)

The polar form is particularly useful in applications involving rotations and oscillations, such as in signal processing and electrical engineering.

3. De Moivre’s Theorem (without proof)

De Moivre’s theorem states that for any complex number expressed in polar form:

Where:

• r = Modulus of the complex number
• θ = Argument (angle) of the complex number

This theorem helps to raise complex numbers to integer powers and plays a crucial role in simplifying expressions involving powers and roots of complex numbers.

Roots of Complex Numbers Using De Moivre’s Theorem

The nth roots of a complex number can be found using De Moivre’s theorem. The formula for finding the nth roots is:

Where:

• k = 0, 1, 2, …, n-1
• n = Number of roots

This formula provides all nth roots of a complex number, evenly spaced on the complex plane. The roots of complex numbers are symmetric with respect to the origin.

4. Circular Functions of Complex Variables

The circular functions of a complex variable are the trigonometric functions extended to complex numbers. These include the familiar sine and cosine functions, which take complex arguments:

These functions are crucial in understanding periodic phenomena in systems where oscillations or waveforms are involved, such as in quantum mechanics or signal processing.

5. Hyperbolic Functions

Hyperbolic functions are analogous to the circular functions but are defined using hyperbolas rather than circles. The two fundamental hyperbolic functions are:

These functions are particularly important in the study of special relativity, heat transfer, and the behavior of systems involving exponential growth or decay.

6. Relations Between Circular and Hyperbolic Functions

There are important relationships between the circular and hyperbolic functions, which show how trigonometric and hyperbolic identities are connected, especially when a complex argument is involved:

These relationships are used in various branches of mathematics and physics, particularly in solving differential equations and in the study of Fourier series.

7. Real and Imaginary Parts of Circular and Hyperbolic Functions

The circular and hyperbolic functions can be separated into their real and imaginary parts when applied to complex arguments. For example, the sine of a complex number \(z = x + iy\) can be expressed as:

This shows how both the real and imaginary components of a complex number influence the outcome of the sine function.

8. Logarithm of Complex Quantities

The logarithm of a complex number \( z = r(cosθ + i * sinθ) \) is given by:

Where:

• r = Modulus of the complex number
• θ = Argument (angle) of the complex number

The complex logarithm is a multi-valued function because the argument \(θ\) can differ by multiples of \(2π\), leading to different “branches” of the logarithm. These branches are essential for correctly defining functions like the complex exponential and logarithmic functions.

Branches of the Complex Logarithm

To define the logarithm of a complex number consistently, a branch of the complex logarithm must be selected. This ensures that the logarithmic function provides a unique value for each input. The principal branch is typically used for simplicity, but other branches are essential in more advanced analysis.

Complex numbers and their associated functions are foundational to many areas of modern mathematics and physics. They allow us to model and solve problems involving two-dimensional vectors, rotations, and oscillations. By mastering their geometric interpretation, De Moivre’s theorem, and the relationships between circular and hyperbolic functions, we gain the tools to tackle more complex systems in both theoretical and applied contexts.

Unit 2: Ordinary Differential Equations of First Order and First Degree and Their Applications

A differential equation is an equation that involves the derivatives of a function. An ordinary differential equation (ODE) is one in which the function involves only one independent variable. If the equation involves only the first derivative of the function (no second or higher derivatives), it is called a first-order differential equation. If the equation is linear in terms of the dependent variable and its derivative, it is called a first-degree equation.

First-order and first-degree differential equations are commonly encountered in various fields of science and engineering. These equations model many real-life phenomena, such as motion, growth, heat transfer, and electrical circuits. Understanding how to solve these equations is essential for analyzing and predicting such systems.

1. Linear Differential Equations

A linear differential equation of the first order is an equation of the form:

Where:

• y is the dependent variable.
• x is the independent variable.
• P(x) and Q(x) are functions of x.

The method to solve this equation involves finding an integrating factor (IF). This is a function that, when multiplied with both sides of the equation, makes the left-hand side an exact derivative of a product of functions.

Integrating Factor

The integrating factor is given by:

Once the integrating factor is determined, multiply both sides of the original differential equation by this factor. The left-hand side will become the derivative of a product:

Now, you can integrate both sides with respect to x to solve for y:

Finally, divide by the integrating factor to find the general solution for y.

Example:

Consider the equation:

In this case, P(x) = 2 and Q(x) = 4. The integrating factor is:

Now, multiply the entire equation by the integrating factor:

The left-hand side is the derivative of y * e^2x, so we can rewrite it as:

Now, integrate both sides with respect to x:

The integral of 4e^2x is 2e^2x. Therefore, the solution is:

Finally, divide by e^2x to get the solution for y:

2. Bernoulli’s Equation

Bernoulli’s equation is a type of nonlinear first-order differential equation. It is of the form:

Here, n is a constant, and yⁿ introduces a nonlinearity to the equation. When n = 0 or n = 1, the equation becomes linear, but for other values of n, it requires special treatment.

To solve Bernoulli’s equation, we use a substitution to convert it into a linear equation. Let:

Then, differentiate both sides with respect to x to get:

Substitute this into the original equation, and it will reduce to a linear form that can be solved using the methods discussed earlier.

Example:

Consider the Bernoulli equation:

Here, n = 2. Let v = y^-1, then dv/dx = -y^-2 * dy/dx. Substituting into the original equation gives:

Rearranging this gives a linear equation in v:

Now solve this linear equation as before using the integrating factor method.

3. Exact Differential Equations

A first-order differential equation of the form:

is called an exact differential equation if there exists a function Φ(x, y) such that:

In this case, the solution can be found by integrating M(x, y) with respect to x and N(x, y) with respect to y. The general solution is given by:

Conditions for Exactness

For an equation to be exact, the following condition must be satisfied:

If this condition is not met, the equation is not exact, but it may still be reducible to an exact equation using an integrating factor.

Example:

Consider the equation:

Here, M(x, y) = 2xy + 3x² and N(x, y) = x² + y. First, check for exactness:

Since ∂M/∂y = ∂N/∂x, the equation is exact. Now, find the potential function Φ(x, y) by integrating M(x, y) with respect to x:

Differentiate this with respect to y and compare with N(x, y) to find g(y), then solve for the general solution.

4. Applications of First-Order Differential Equations

Orthogonal Trajectories

Orthogonal trajectories are curves that intersect a given family of curves at right angles (i.e., perpendicularly). These are often used in physics and engineering to model orthogonal relationships between different physical quantities. For example, orthogonal trajectories can represent electric field lines that are perpendicular to equipotential surfaces.

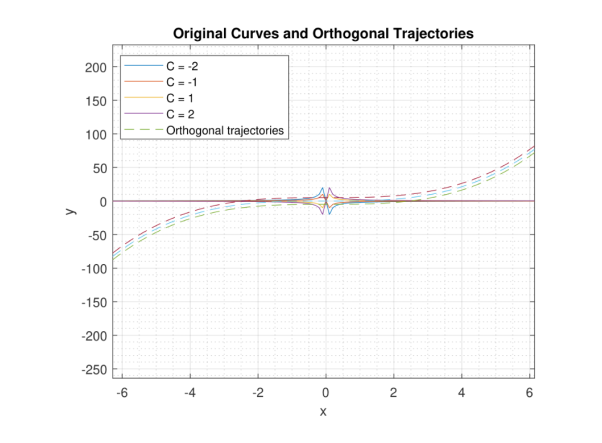
To find the orthogonal trajectories of a given family of curves, first determine the differential equation representing the family. Then, find the negative reciprocal of the slope (derivative) of the given family of curves. This gives the differential equation for the orthogonal trajectories. Solve this new differential equation to find the orthogonal curves.

Mechanical Systems

Mechanical systems often involve forces and motion described by first-order differential equations. For instance, the velocity of an object subjected to air resistance can be modeled by a first-order differential equation. The general form for such systems is:

Where m is the mass of the object, v is the velocity, b is the damping coefficient, and F(t) is an external force. This equation can be solved to find the velocity as a function of time.

Electrical Systems

In electrical circuits, first-order differential equations describe the behavior of components like resistors, capacitors, and inductors. For example, the charging of a capacitor in an RC circuit is governed by the equation:

Where q is the charge on the capacitor, R is the resistance, C is the capacitance, and E(t) is the voltage source. Solving this equation gives the charge as a function of time.

Unit 3: Linear Differential Equations with Constant Coefficients

Linear differential equations with constant coefficients are a specific type of differential equation that plays a critical role in various applications, including physics, engineering, and mathematics. These equations typically take the form:

Where:

• y⁽ⁿ⁾ is the nth derivative of the function y(t).
• a_i are constant coefficients.
• f(t) is a given function of t, which is the non-homogeneous part of the equation.

1. Introductory Remarks

The solution to a linear differential equation can be expressed as the sum of two parts:

• Complementary Function (CF): The solution of the associated homogeneous equation.
• Particular Integral (PI): A specific solution to the non-homogeneous equation.

Complementary Function

To find the complementary function, we solve the homogeneous equation:

This typically involves finding the characteristic equation:

The roots of this equation determine the form of the complementary function:

• If the roots are real and distinct, CF = C₁e^r₁t + C₂e^r₂t + …
• If the roots are real and repeated, CF = (C₁ + C₂t)e^r₁t
• If the roots are complex, CF = e^αt(C₁cos(βt) + C₂sin(βt)), where r = α ± βi.

Particular Integral

The particular integral is determined based on the form of the non-homogeneous part f(t). There are several methods to find the particular integral, including:

• Method of Undetermined Coefficients: Suitable for polynomial, exponential, sine, and cosine functions.
• Variation of Parameters: A more general method that can be applied to a wider range of functions.

2. Rules for Finding Complementary Functions and Particular Integrals

Method of Undetermined Coefficients

This method is used when f(t) is a polynomial, exponential, or trigonometric function. The basic idea is to guess the form of the particular integral based on f(t) and determine the coefficients by substituting back into the original equation.

Example:

Consider the equation:

Here, we guess a particular integral of the form:

Substitute y_p into the equation to find A. The complementary function is found from the associated homogeneous equation:

3. Method of Variation of Parameters

This method can be used for any non-homogeneous term f(t). Instead of using constant coefficients for the complementary function, we allow them to vary:

Where u_i are functions of t and y_i are the solutions of the complementary function. To find u_i, we solve the following equations:

This method provides a systematic way to obtain the particular integral without guessing its form.

4. Cauchy’s Homogeneous and Legendre’s Linear Equations

Cauchy’s Homogeneous Equation

A Cauchy’s homogeneous equation is of the form:

To solve this type of equation, we use the substitution:

This leads to a characteristic equation in terms of m that can be solved for its roots, and the general solution is constructed similarly as before based on the roots obtained.

Legendre’s Linear Equation

Legendre’s linear equation has the form:

This equation is commonly encountered in physics and engineering, especially in problems involving spherical coordinates. The solutions to this equation are known as Legendre polynomials, denoted by P_n(x).

Linear differential equations with constant coefficients are a foundational topic in differential equations. Understanding the methods to find the complementary function and particular integral is essential for solving these equations effectively. With applications across various scientific fields, mastering these techniques enables better problem-solving and analytical skills.

Unit 4: Fourier Series

The Fourier series is a powerful mathematical tool used to represent periodic functions as sums of sines and cosines. It plays a significant role in various fields, including signal processing, heat transfer, and vibration analysis. By breaking down complex periodic functions into simpler trigonometric components, we can analyze and manipulate them more effectively.

1. Introductory Remarks

The general form of the Fourier series expansion of a function f(t) defined on the interval [-L, L] is given by:

Where:

• ω_n = n(π/L) is the fundamental frequency.
• a₀ = (1/2L) ∫_-L^L f(t) dt is the average value of the function over the interval.
• a_n = (1/L) ∫_-L^L f(t)cos(ω_nt) dt are the coefficients for the cosine terms.
• b_n = (1/L) ∫_-L^L f(t)sin(ω_nt) dt are the coefficients for the sine terms.

2. Euler’s Formulae

Euler’s formula provides a relationship between complex exponentials and trigonometric functions, given by:

This formula allows us to express Fourier series in terms of complex exponentials, which can simplify calculations. The Fourier series can also be written as:

Where c_n are complex coefficients derived from the original coefficients:

3. Conditions for Fourier Series Expansion

For a function to be expressed as a Fourier series, it must satisfy certain conditions known as Dirichlet’s conditions:

• The function must be periodic.
• The function must be piecewise continuous on the interval.
• The function must have a finite number of discontinuities within one period.

These conditions ensure that the Fourier series converges to the function at most points in the interval.

Functions Having Points of Discontinuity

If a function has points of discontinuity, the Fourier series will converge to the average of the left-hand and right-hand limits at those points. This phenomenon is known as the Gibbs phenomenon, where the series overshoots at the discontinuities.

4. Change of Interval

If the function is defined on a different interval, say [a, b], we can adjust the Fourier series accordingly:

This adaptation allows the Fourier series to fit a wider range of functions.

5. Odd and Even Functions

When dealing with Fourier series, it’s useful to classify functions as odd or even:

• • Odd Functions: Functions that satisfy f(-t) = -f(t). Their Fourier series contains only sine terms:

• • Even Functions: Functions that satisfy f(-t) = f(t). Their Fourier series contains only cosine terms:

This classification can simplify the process of finding the Fourier series.

6. Half-Range Series

When a function is defined on a half-interval, such as [0, L], we can construct half-range sine and cosine series:

• • Half-Range Sine Series (for functions defined on [0, L]):

• • Half-Range Cosine Series (for functions defined on [0, L]):

These series are particularly useful in applications where the function is defined over a limited range, allowing for an efficient representation of the function.

Fourier series provide a powerful method for representing periodic functions as sums of sines and cosines. Understanding the conditions for expansion, the role of Euler’s formula, and the distinctions between odd and even functions is crucial for effectively applying this concept in various fields, from engineering to physics.

Unit 5: Vector Calculus

Vector calculus is a branch of mathematics that deals with vector fields and the differentiation and integration of vector functions. It is fundamental in physics and engineering, particularly in fields like fluid dynamics, electromagnetism, and mechanics. This document covers scalar and vector fields, the gradient, divergence, curl, solenoidal and irrotational fields, vector identities, and key theorems in vector calculus.

1. Scalar and Vector Fields

A scalar field is a function that assigns a single scalar value to every point in space. Examples include temperature and pressure. A vector field, on the other hand, assigns a vector to every point in space, representing quantities like velocity and force.

Here, F is a vector field defined in three-dimensional space, where P, Q, and R are scalar functions representing the components of the vector at point (x, y, z).

2. Gradient

The gradient of a scalar field φ is a vector field that points in the direction of the greatest rate of increase of the scalar field. It is defined as:

The components of the gradient vector are the partial derivatives of φ with respect to each spatial variable. The magnitude of the gradient indicates the steepness of the field.

3. Divergence

The divergence of a vector field F measures the rate at which “stuff” is expanding out of a point. It is defined as:

Here, F = P i + Q j + R k. A positive divergence indicates a source, while a negative divergence indicates a sink.

4. Curl

The curl of a vector field F represents the amount of rotation or the tendency to induce rotation at a point. It is defined as:

This expression gives a vector that points in the direction of the axis of rotation, and its magnitude represents the strength of that rotation.

5. Solenoidal and Irrotational Fields

A vector field is called solenoidal if its divergence is zero:

This condition indicates that the vector field has no sources or sinks and is typically associated with incompressible fluid flow.

A vector field is irrotational if its curl is zero:

This condition implies that the field has no rotational components and is often found in potential flow situations.

6. Vector Identities

Various vector identities are useful in vector calculus. Here are some key identities (statements only, without proofs):

• ∇·(A × B) = B·(∇ × A) – A·(∇ × B)
• ∇ × (A × B) = A(∇·B) – B(∇·A) + (B·∇)A – (A·∇)B
• ∇·(∇φ) = ∇²φ (Laplacian operator)

7. Key Theorems

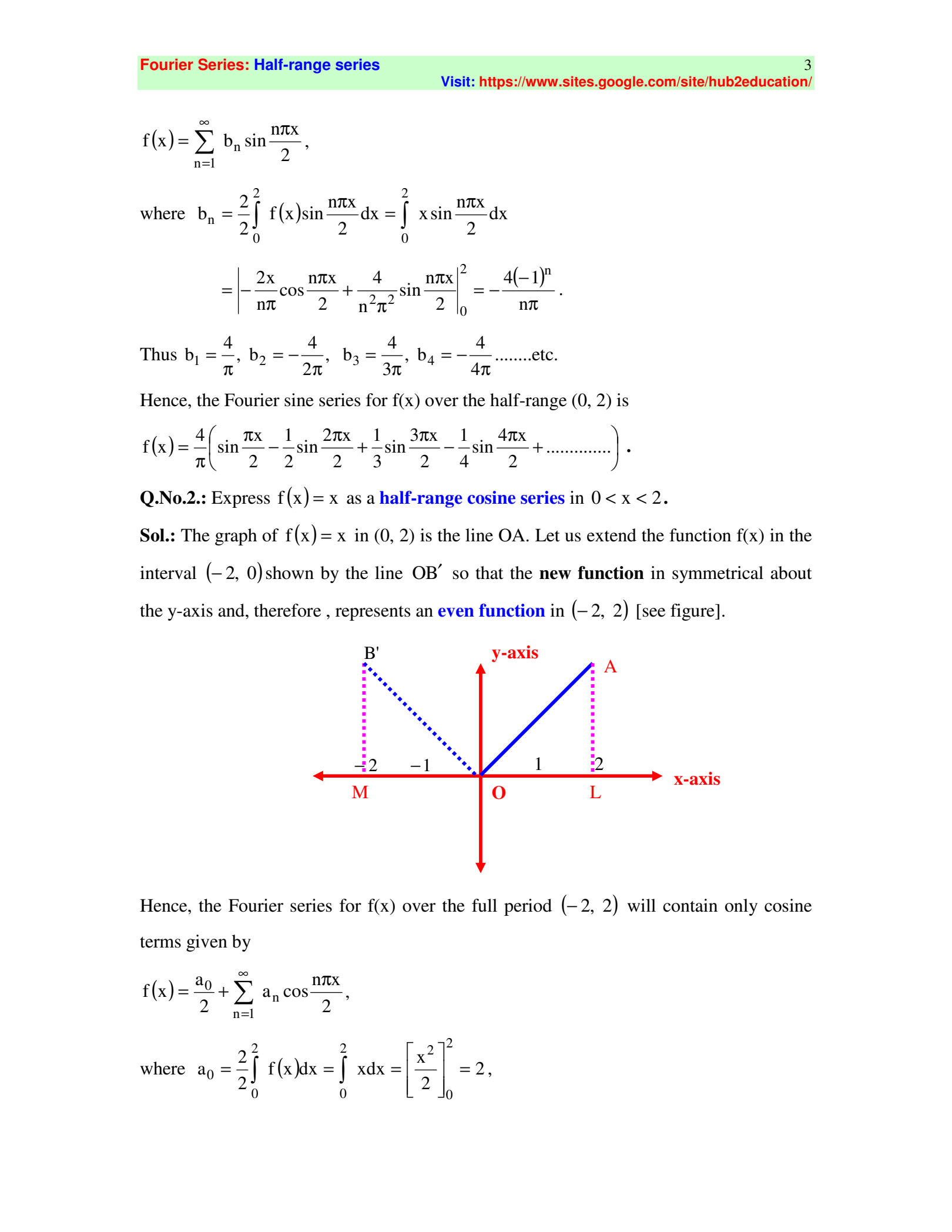
Green’s Lemma

Green’s Theorem relates a double integral over a region R to a line integral around its boundary C:

This theorem is useful in converting between line integrals and double integrals, particularly in planar regions.

Gauss’ Divergence Theorem

Gauss’ Theorem connects the flow of a vector field through a closed surface to the divergence over the volume enclosed by the surface:

Here, S is the surface bounding the volume V. This theorem is vital in physics, particularly in electromagnetism.

Stokes’ Theorem

Stokes’ Theorem relates a surface integral of the curl of a vector field over a surface S to a line integral around the boundary C:

This theorem is instrumental in converting surface integrals into line integrals, simplifying the evaluation of complex integrals.

Vector calculus is a powerful mathematical framework that allows for the analysis and interpretation of vector fields in various physical contexts. Understanding concepts like gradient, divergence, curl, and the various theorems provides essential tools for applications in physics and engineering.

fig=Vector Field Diagram⬆

fig=Gradient, Divergence, and Curl⬆

fig-Green’s Theorem Diagram⬆

fig-Gauss’ Divergence Theorem Diagram⬆

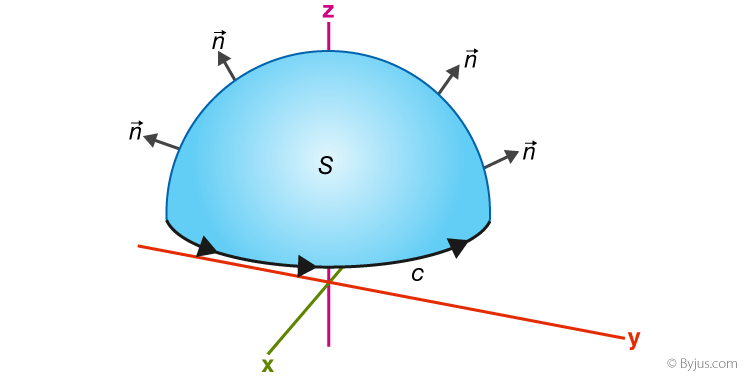
fig-Stokes’ Theorem Diagram⬆

Text Books:

a. Higher Engineering Mathematics by B. S. Grewal, Khanna Publishers, NewDelhi.
b. Advanced Engineering Mathematics by Erwin Kreyszig, John Wiley & Sons, NewYork.
c. A Course in Engineering Mathematics (Vol II) by Dr. B. B. Singh, Synergy Knowledge
ware,Mumbai.
d. A Text Book of Applied Mathematics (Vol I & II) by P. N. Wartikar and J. N. Wartikar, Pune
Vidyarthi Griha Prakashan,Pune.
e. Higher Engineering Mathematics by H. K. Das and Er. Rajnish Verma, S. Chand & CO. Pvt.
Ltd., New Delhi.

Reference Books:

a. Higher Engineering Mathematics by B. V. Ramana, Tata McGraw-Hill Publications, New
Delhi.
b. A Text Book of Engineering Mathematics by Peter O‟ Neil, Thomson Asia Pte Ltd. , Singapore.
c. Advanced Engineering Mathematics by C. R. Wylie & L. C. Barrett, Tata Mcgraw-Hill
Publishing Company Ltd., NewDelhi.