Unit 1: Laplace Transform

1. Definition of Laplace Transform

The Laplace Transform of a function f(t) is defined as:

where:

• t: Time-domain variable
• s: Complex frequency-domain variable
• f(t): The original function
• F(s): The Laplace transform of f(t)

2. Conditions for Existence of the Laplace Transform

A function f(t) is said to have a Laplace Transform if the integral:

exists and converges. This typically requires that f(t) be of exponential order.

3. Laplace Transform of Elementary Functions

The Laplace Transforms of common elementary functions are:

• 1. L{1} = 1/s
• 2. L{t} = 1/s²
• 3. L{tⁿ} = n!/sⁿ⁺¹
• 4. L{e^at} = 1/(s – a)
• 5. L{cos(at)} = s/(s² + a²)
• 6. L{sin(at)} = a/(s² + a²)

4. Properties of Laplace Transforms

4.1 Linearity Property

If L{f(t)} = F(s) and L{g(t)} = G(s), then:

This means that the Laplace Transform of a linear combination of functions is the same linear combination of their transforms.

4.2 First Shifting Property

If L{f(t)} = F(s), then:

This property shifts the s-variable in the transform by a.

4.3 Second Shifting Property (Heaviside Unit Step Function)

The Heaviside function U(t – a) equals 0 for t < a and 1 for t ≥ a. If L{f(t)} = F(s), then:

4.4 Scaling Property

If L{f(t)} = F(s), then for any constant a:

4.5 Transforms of Derivatives

If L{f(t)} = F(s), then the Laplace Transform of the derivative is:

5. Special Functions

5.1 Heaviside (Unit Step) Function

The Heaviside function U(t – a) “steps” from 0 to 1 at t = a. Its Laplace Transform is:

5.2 Dirac Delta Function

The Dirac delta function, δ(t – a), is 0 everywhere except at t = a, where it is infinite, with the property that:

Its Laplace Transform is:

6. Evaluation of Integrals Using Laplace Transform

Laplace Transforms can also be used to evaluate certain definite integrals. For example:

This is derived from the basic properties of Laplace Transforms.

7. Application of Laplace Transforms in Solving Differential Equations

The Laplace Transform is widely used to solve linear ordinary differential equations (ODEs). By transforming the ODE from the time domain to the s-domain, we convert it into an algebraic equation, which is easier to solve.

Example:

Consider the ODE: m d²x/dt² + b dx/dt + kx = F(t) (Equation of motion for a damped harmonic oscillator).

By applying the Laplace Transform:

This is a simpler algebraic equation in terms of X(s), the Laplace Transform of the displacement x(t).

8. Diagrams for Visualization

To visualize concepts like the Unit Step Function or Dirac Delta Function, diagrams can be helpful:

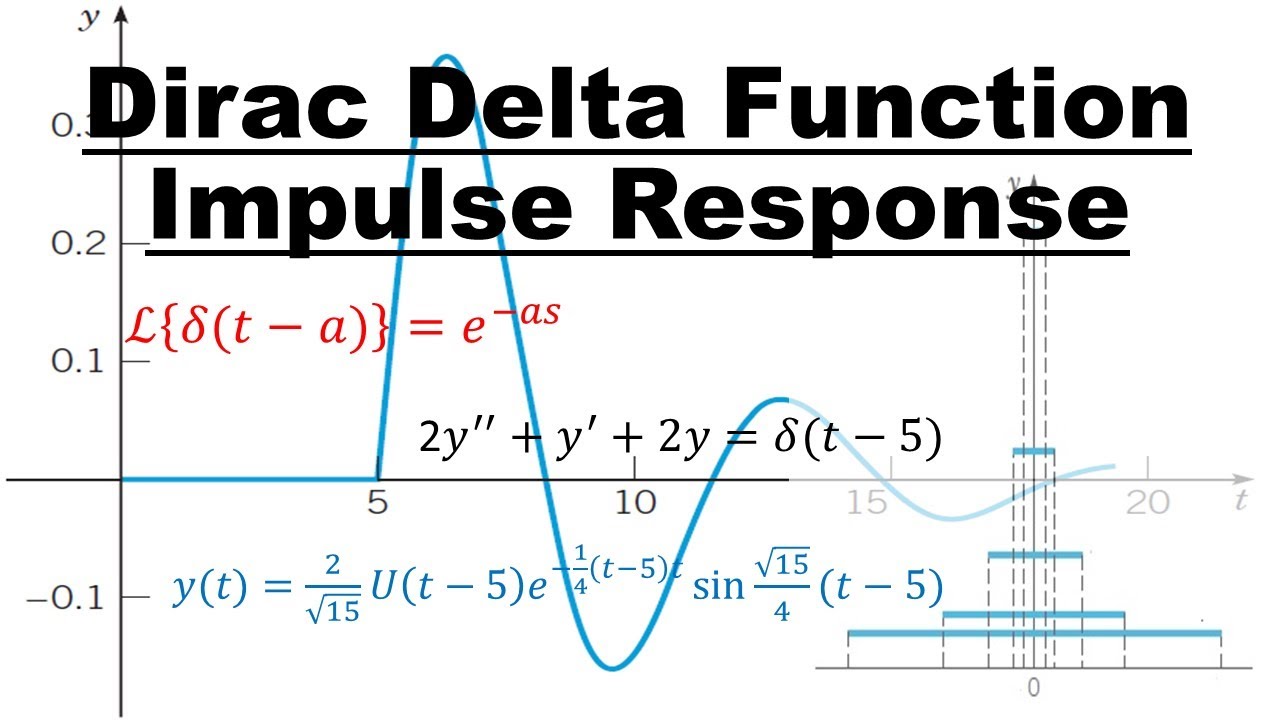
Figure 1: Dirac Delta Function

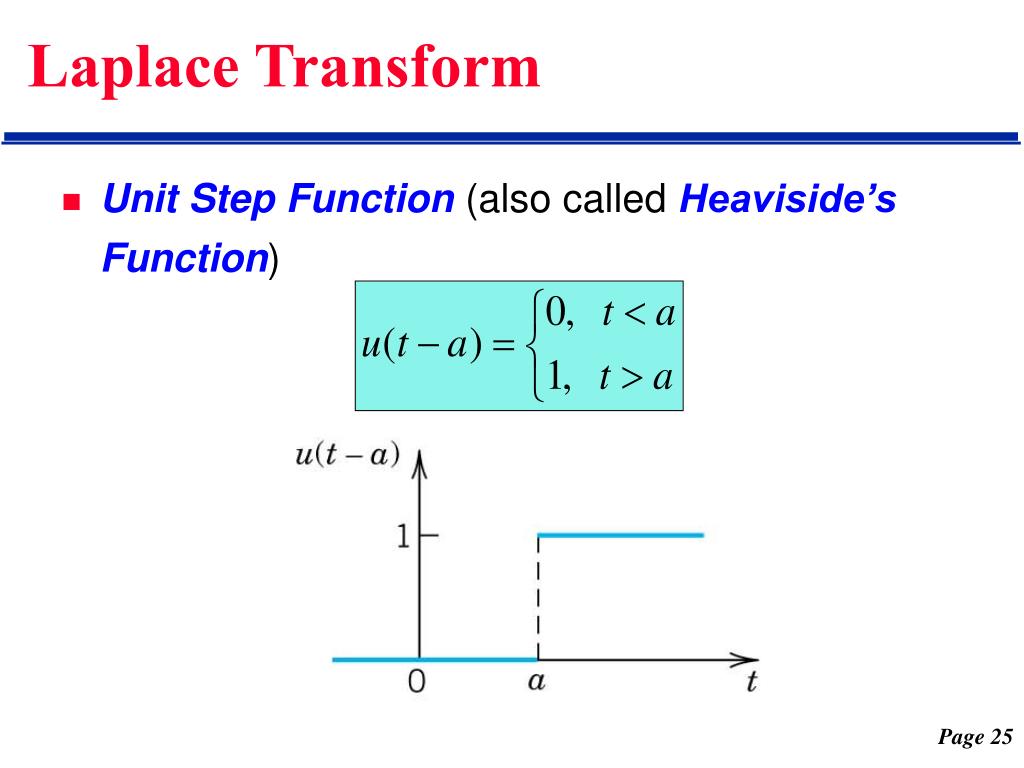
Figure 2: Heaviside Unit Step Function

Unit 2: Inverse Laplace Transform

1. Introductory Remarks

The Inverse Laplace Transform is a technique used to revert a function in the Laplace domain (frequency domain) back to the time domain. If F(s) is the Laplace Transform of f(t), then:

This process is crucial for solving linear differential equations and engineering problems that are expressed in terms of Laplace transforms.

2. Inverse Transforms of Some Elementary Functions

Here are some common elementary functions and their corresponding inverse Laplace transforms:

• 1. L^-1{1/s} = 1
• 2. L^-1{1/s²} = t
• 3. L^-1{n!/sⁿ⁺¹} = tⁿ
• 4. L^-1{1/(s – a)} = e^at
• 5. L^-1{s/(s² + a²)} = cos(at)
• 6. L^-1{a/(s² + a²)} = sin(at)

3. General Methods of Finding Inverse Transforms

3.1 Direct Inversion Using Known Transforms

The simplest method is to refer to a table of known Laplace Transforms and apply the inverse based on the function form of F(s). This method works well for basic or standard transforms.

3.2 Partial Fraction Expansion Method

When dealing with rational functions, where F(s) is a ratio of polynomials, the function is decomposed into partial fractions. Each fraction can then be inverted using known inverse Laplace Transforms.

Example: Find the inverse Laplace transform of F(s) = (2s + 3)/(s² + 3s + 2).

We can factor the denominator:

Next, apply partial fraction decomposition:

Solving for A and B:

• Multiply both sides by (s + 1)(s + 2)
• Set values of s to cancel out the terms and solve for A and B
• Finally, use inverse transforms on each term: L^-1{A/(s + 1)} = A e^-t

3.3 Convolution Theorem

For more complex functions, the Convolution Theorem is helpful. If F(s) = F₁(s) F₂(s), then:

This represents the convolution of f₁(t) and f₂(t).

4. Applications in Solving Linear Differential Equations

4.1 Solving First-Order Differential Equations

Consider the first-order differential equation:

To solve this using the Laplace Transform:

• • Take the Laplace Transform of both sides:

• • Solve for Y(s):

• Finally, take the inverse Laplace Transform to find y(t).

4.2 Solving Second-Order Differential Equations

Consider the second-order differential equation:

To solve:

• • Take the Laplace Transform:

• • Solve for X(s):

• Take the inverse Laplace Transform to find x(t).

4.3 Simultaneous Linear Differential Equations

Laplace Transforms are also useful in solving systems of simultaneous linear differential equations. By taking the Laplace Transform of each equation, you can convert the system into algebraic equations, solve for the Laplace Transforms of each variable, and then apply inverse transforms to find the solution.

5. Diagrams for Visualization

In systems governed by differential equations, the solution is often a time-domain function. Visualization of these functions can help in understanding behavior over time:

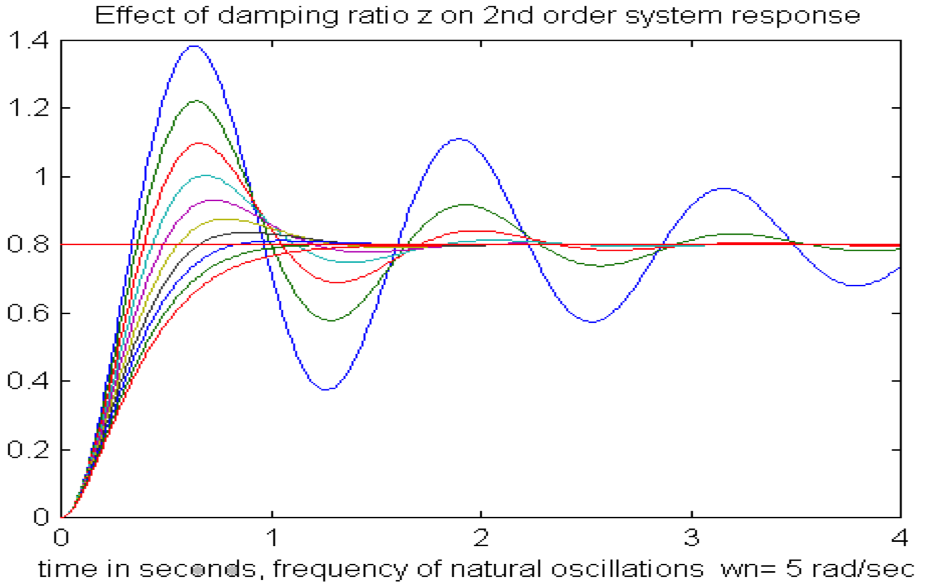
Figure 1: Response of an underdamped oscillator, solved using Laplace transforms.

Unit 3: Fourier Transform and Lasers

Fourier Transform

The Fourier Transform is a mathematical technique used to transform a time-domain signal into its corresponding frequency-domain representation. It is widely used in signal processing, physics, and engineering to analyze the frequency content of signals.

1. Integral Transforms

An integral transform is a mathematical operation that converts a function into another function via an integral. The most well-known integral transforms include the Fourier Transform, Laplace Transform, and Z-Transform.

2. Fourier Integral Theorem

The Fourier integral theorem states that any piecewise continuous function can be represented as an integral of sine and cosine terms. This theorem is the foundation of Fourier analysis.

Explanation: The function \( f(t) \) is represented as the inverse Fourier transform of \( F(\omega) \), where \( \omega \) is the angular frequency, and the exponential term includes the complex representation of oscillatory functions (sine and cosine).

3. Fourier Sine and Cosine Integrals

The Fourier sine and cosine integrals express a function in terms of sine and cosine waves. These integrals are useful when dealing with functions that are not symmetric around the origin.

Explanation: The sine integral represents a function \( f(t) \) in terms of sine functions. Similarly, we can write the cosine integral as:

These are used when the function is odd (for sine) or even (for cosine).

4. Complex Form of Fourier Integrals

The Fourier transform can be expressed in its complex form using Euler’s formula, which relates the sine and cosine terms to a complex exponential. This is convenient for many practical applications.

Explanation: This formula shows that the function \( f(t) \) can be reconstructed using the complex exponential term, where \( F(\omega) \) is the frequency-domain representation.

5. Fourier Sine and Cosine Transforms

The Fourier sine and cosine transforms are specific cases of the Fourier transform where the function is multiplied by sine or cosine, respectively. These transforms are used to analyze signals with specific boundary conditions.

Explanation: These transforms are useful when the original signal is either odd (for sine) or even (for cosine). They provide a way to analyze specific types of signals.

6. Properties of Fourier Transforms

The Fourier transform has several useful properties, including:

• Linearity: The Fourier transform of a linear combination of functions is the same linear combination of their Fourier transforms.
• Time Shifting: Shifting a function in time results in a phase shift in its Fourier transform.
• Frequency Shifting: Modulating a function by a sinusoidal signal results in a shift in frequency.

Explanation: This formula represents the time-shifting property. Shifting the function \( f(t) \) by \( t_0 \) results in multiplying the Fourier transform \( F(\omega) \) by a phase factor.

7. Parseval’s Identity for Fourier Transforms

Parseval’s identity states that the total energy of a signal in the time domain is equal to the total energy in the frequency domain. This property is particularly useful in signal processing and communications.

Explanation: Parseval’s identity shows the conservation of energy between time-domain and frequency-domain representations of a signal.

Principle of Laser, Types of Lasers, and Applications

1. Principle of Laser

A laser (Light Amplification by Stimulated Emission of Radiation) operates based on the principle of stimulated emission. When an electron in an excited state is stimulated by an external photon, it releases a photon of the same energy, resulting in amplified light.

The key components of a laser include:

• Active Medium: The material where laser action takes place, such as a ruby crystal or gas mixture.
• Pumping Source: Provides the energy required to excite electrons in the active medium.
• Optical Cavity: Consists of mirrors that reflect light back and forth, amplifying the emitted photons.

2. Types of Lasers

Ruby Laser

A ruby laser is a solid-state laser that uses a synthetic ruby crystal (aluminum oxide with chromium ions) as its active medium. The chromium ions absorb green and blue light, and emit red light at a wavelength of 694.3 nm.

Working: The ruby laser is a three-level laser system. When the ruby crystal is pumped with light from a flash lamp, electrons in the chromium ions are excited to higher energy levels. As they return to the ground state, they emit coherent light.

Applications:

• Holography
• Medical applications (e.g., eye surgery)
• Material cutting and welding

Helium-Neon (He-Ne) Laser

The helium-neon laser is a gas laser that uses a mixture of helium and neon gases as the active medium. It emits light at a wavelength of 632.8 nm, which is visible red light.

Working: An electrical discharge excites helium atoms, which in turn transfer their energy to neon atoms via collisions. The neon atoms then emit coherent light as they transition between energy levels.

Applications:

• Barcode scanning
• Laser pointers
• Interferometry

Lasers play an important role in a wide range of applications, including communications, medicine, manufacturing, and scientific research.

Unit 4: Partial Differential Equations and Their Applications

1. Formation of Partial Differential Equations (PDEs)

Partial Differential Equations (PDEs) involve partial derivatives of a function with respect to two or more independent variables. PDEs can describe various physical phenomena such as heat conduction, fluid dynamics, and wave propagation.

1.1 Elimination of Arbitrary Constants

A PDE can be formed by eliminating arbitrary constants from a given equation. Suppose you have a function with arbitrary constants, differentiating it with respect to the variables and eliminating the constants will give a PDE.

Example:

Consider the equation z = ax + by + c, where **a**, **b**, and **c** are arbitrary constants. By differentiating this equation with respect to **x** and **y**:

Eliminating **a** and **b** gives us the PDE:

1.2 Elimination of Arbitrary Functions

PDEs can also be formed by eliminating arbitrary functions. This is done by differentiating and eliminating arbitrary functions through substitutions.

2. Equations Solvable by Direct Integration

Some first-order PDEs can be solved directly by integration. These equations are generally of the form:

In such cases, integrating both sides of the equation will give the solution. These types of PDEs are straightforward and solvable by applying integration rules.

3. Linear Equations of First Order (Lagrange’s Linear Equations)

Lagrange’s linear equations are first-order PDEs of the form:

Where **P**, **Q**, and **R** are functions of **x**, **y**, and **z**. The general solution to Lagrange’s equation involves using the method of characteristics to reduce the PDE to an ordinary differential equation (ODE).

4. Method of Separation of Variables

The **method of separation of variables** is a powerful technique for solving PDEs. It assumes that the solution can be written as the product of functions, each depending on a single variable. This allows us to break down a PDE into simpler ordinary differential equations (ODEs).

4.1 One-Dimensional Heat Flow Equation

The **one-dimensional heat equation** describes how heat flows through a rod over time. It is given by:

Here, **u(x, t)** represents the temperature at point **x** and time **t**, and **α** is the thermal diffusivity constant.

Using the method of separation of variables, we assume that **u(x, t)** can be written as a product of two functions:

Substituting this into the heat equation and separating the variables gives us two ODEs:

Solving these equations will yield the solution to the heat flow problem.

4.2 One-Dimensional Wave Equation

The **one-dimensional wave equation** describes the motion of a vibrating string. It is given by:

Here, **u(x, t)** represents the displacement of the string at point **x** and time **t**, and **c** is the wave speed.

Again, using separation of variables, we assume:

Substituting this into the wave equation gives us two ODEs that can be solved separately:

5. Diagram of Heat Flow and Wave Equation

The following diagrams illustrate the physical significance of the heat flow equation and wave equation:

Figure 1: Temperature distribution in a rod over time as per the heat equation.

Figure 2: Vibration of a string as described by the wave equation.

Unit 5: Functions of Complex Variables

1. Analytic Functions

An **analytic function** is a complex function that is differentiable at every point in its domain. For a complex function f(z), where z = x + iy, the function is said to be analytic if it satisfies the Cauchy-Riemann equations.

If a function is analytic, it has derivatives of all orders, and this makes it behave similarly to a real-valued function. Functions such as polynomials, exponentials, and trigonometric functions are examples of analytic functions in the complex domain.

2. Cauchy-Riemann Equations

The **Cauchy-Riemann equations** provide a set of conditions that must be satisfied for a complex function to be differentiable and hence analytic. These equations relate the real and imaginary parts of a complex function.

2.1 Cartesian Form

Let the complex function be f(z) = u(x, y) + iv(x, y), where **u(x, y)** and **v(x, y)** are the real and imaginary parts of the function, respectively. The Cauchy-Riemann equations in Cartesian form are:

2.2 Polar Form

In polar coordinates, where z = r(cosθ + i sinθ) and **r** and **θ** are the polar coordinates of **z**, the Cauchy-Riemann equations are modified to account for the radial and angular components:

3. Harmonic Functions

A **harmonic function** is a twice continuously differentiable function that satisfies Laplace’s equation. For a complex function to be harmonic, both the real and imaginary parts must satisfy the following Laplace equation:

These conditions ensure that the function is smooth and exhibits harmonic behavior in both the real and imaginary parts.

4. Cauchy’s Integral Theorem

**Cauchy’s Integral Theorem** is one of the fundamental results in complex analysis. It states that if a function **f(z)** is analytic in a simply connected domain and along a closed curve **C**, then the integral of the function around **C** is zero:

This theorem is important because it leads to several other results in complex analysis, including Cauchy’s integral formula and the residue theorem.

5. Cauchy’s Integral Formula

**Cauchy’s Integral Formula** provides the value of a function at any point within a domain based on the values of the function along a surrounding closed curve. If **f(z)** is analytic inside and on a simple closed contour **C**, and **z₀** is a point inside **C**, then:

This formula allows us to compute the value of an analytic function at any point within a region where the function is analytic.

6. Residues

The **residue** of a function **f(z)** at a singularity is the coefficient of **(1/(z – z₀))** in the Laurent series expansion of the function. It plays a crucial role in evaluating complex integrals using the residue theorem.

If **f(z)** has a singularity at **z₀**, then the residue at **z₀** is given by:

This formula simplifies the calculation of integrals by focusing on the behavior of the function around singularities.

7. Cauchy’s Residue Theorem

**Cauchy’s Residue Theorem** is a powerful tool for evaluating contour integrals in the complex plane. It states that if **f(z)** is analytic in a region except for isolated singularities inside a contour **C**, the integral of **f(z)** around **C** is equal to **2πi** times the sum of the residues at those singularities:

This theorem is particularly useful when calculating complex integrals in cases where the function has poles inside the contour.

Diagrams

The following diagrams represent important concepts in complex analysis:

Figure 1: The complex plane, showing real and imaginary axes.

Figure 2: Contour **C** enclosing singularities where the residue theorem applies.

Text Books

• Higher Engineering Mathematics by B. S. Grewal, Khanna Publishers, New Delhi.
• Higher Engineering Mathematics by H. K. Das and Er. Rajnish Verma, S. Chand & CO. Pvt. Ltd., New Delhi.
• A Course in Engineering Mathematics (Vol III) by Dr. B. B. Singh, Synergy Knowledge ware, Mumbai.
• Higher Engineering Mathematics by B. V. Ramana, Tata McGraw-Hill Publications, New Delhi.

Reference Books

• Advanced Engineering Mathematics by Erwin Kreyszig, John Wiley & Sons, New York.
• A Text Book of Engineering Mathematics by Peter O’ Neil, Thomson Asia Pte Ltd., Singapore.
• Advanced Engineering Mathematics by C. R. Wylie & L. C. Barrett, Tata McGraw-Hill Publishing Company Ltd., New Delhi.
• Integral Transforms and Their Engineering Applications by Dr. B. B. Singh, Synergy Knowledge ware, Mumbai.
• Integral Transforms by I. N. Sneddon, Tata McGraw-Hill, New York.